import numpy as np
import math
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
from matplotlib.animation import FuncAnimation, FFMpegWriter, PillowWriter
from IPython.display import HTML
dtype = torch.float32
device = torch.device('cuda:0') if torch.cuda.is_available() else torch.device('cpu')
This jupyter notebook can be found here: https://github.com/cagatayyildiz/pca-ae-vae-diffmodels.
0. References¶
This presentation contains many ideas, re-phrased sentences and screenshots from the following resources, particularly the first two:
1. Diffusion models¶
The main idea behind diffusion models is the following:

Forward model: Here, we first implement a forward model $q(x_t | x_{t-1})$ that transforms samples from a complicated (data) distribution into a simple, tractable distribution (Gaussian). The process is Markovian. Later, we will specify the hyperparameters involved in this process.
Backward model: Inverting the forward model lets us generate samples from the initial data distributions. This can be done by learning a neural network that inverts the forward step, thereby denoises.
$\newcommand{\E}[2][]{ \mathbb{E}_{#1}\left[ #2 \right] }$ $\newcommand{\N}{\mathcal{N}}$ $\newcommand{\hb}[3]{ \frac {\textrm{d}^{#1}{#2}} {\textrm{d}{#3}} }$
1.1. Forward model¶
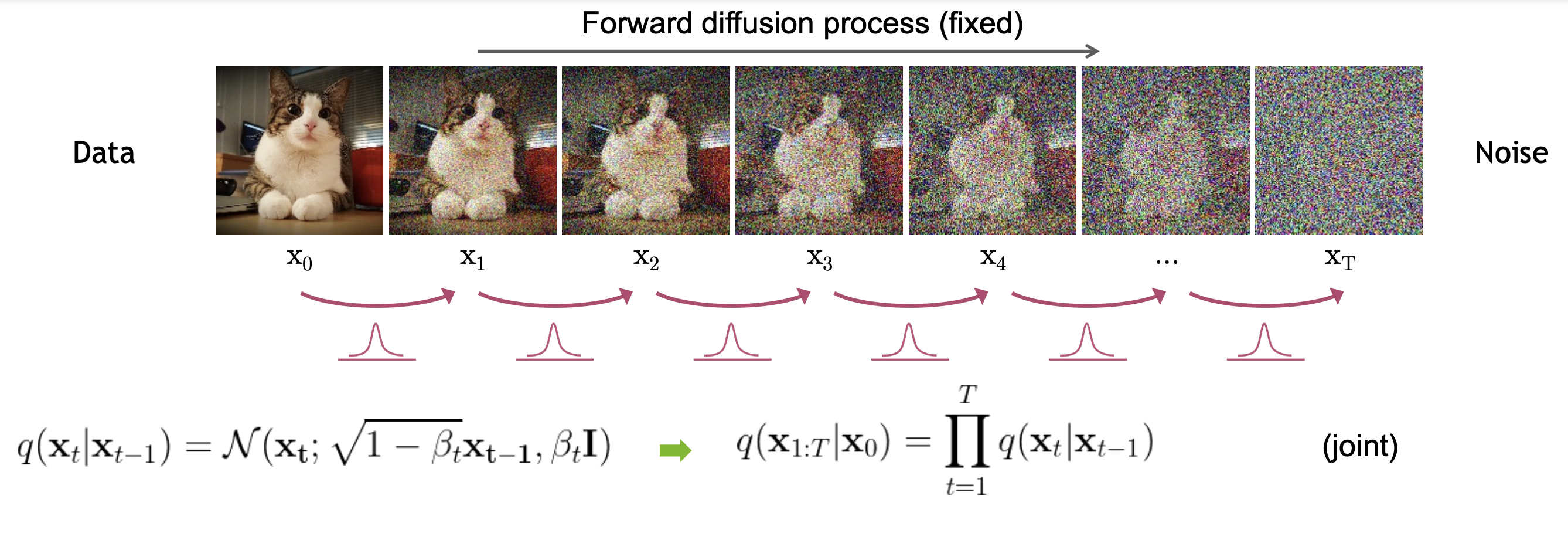
1.1.1. Diffusion example with fixed updates¶
Given a dataset
$$ \mathcal{D} = \{x_0^{(1)}, x_0^{(2)}, \dots, x_0^{(N)}\},$$
we consider an empirical data distribution:
$$ q(x_0) = \pi(x_0) = \frac{1}{N}\sum_{i=1}^{N} \delta(x_0 - x_0^{(i)}).$$
Diffusion models start from an initial realization $x_0$ from an empirical data distribution $\pi(x_0)$. Then, they iteratively rescale by a factor $0 < a < 1$ and add noise $\epsilon_t \sim \N(0, 1)$ at each step:
\begin{align} &0 < a < 1 \\ x_0 & \sim \pi(x_0) \\ t & = 1,2,\dots \\ \epsilon_t &\sim \N(0, 1) \\ x_t & = a x_{t-1} + \sigma \epsilon_t, \end{align}
which then implies the following factorization:
\begin{align} q(x_{0:T}) = q(x_0) \prod_{t=1}^T q(x_t \mid x_{t-1}). \end{align}
Here, $x_0$ has a Dirac mass, meaning that $x_1$ would follow a Gaussian distribution. Since Gaussians are closed under linear operations, all $x_i$ stays Gaussian. Let's see how the flow goes on:
\begin{align} x_1 & = a x_{0} + \sigma \epsilon_1 \\ x_2 & = a (a x_{0} + \sigma \epsilon_1) + \sigma \epsilon_2 = a^2 x_{0} + a\sigma \epsilon_1 + \sigma \epsilon_2\\ x_3 & = a (a (a x_{0} + \sigma \epsilon_1) + \sigma \epsilon_2) + \sigma \epsilon_3 = a^3 x_{0} + a^2 \sigma \epsilon_1 + a \sigma \epsilon_2 + \sigma \epsilon_3\\ \dots \\ x_t & = a^t x_{0} + \sigma(a^{t-1} \epsilon_1 + a^{t-2} \epsilon_2 + \dots + a \epsilon_{t-1} + \epsilon_t). \end{align}
Next, we compute the statistics of $x_t$. Conveniently, we have a closed form expression for the mean of $x_t$:
\begin{align} \E[\epsilon]{x_t|x_0} & = a^t x_{0}. \end{align}
To compute the variance, we first note
\begin{align} x_t - \E{x_t|x_0} & = \sigma(a^{t-1} \epsilon_1 + a^{t-2} \epsilon_2 + \dots + a \epsilon_{t-1} + \epsilon_t). \end{align}
Next, we look at the square
\begin{align} \left(x_t - \E{x_t|x_0} \right)^2 & = \sigma^2 \left( \sum_{i=1}^t(a^{t-i})^2\epsilon_i^2 + \sum_{i,j=1}^t (a^{2t-i-j})\epsilon_i\epsilon_j \right) \end{align}
Noting that
$$\E{\epsilon_t^2} = 1 \quad\text{and}\quad \E{\epsilon_t \epsilon_\tau } = 0, ~ t \neq \tau, $$
the expectation becomes
\begin{align} \E{(x_t - \E{x_t|x_0})^2} & = \sigma^2 \sum_{i=0}^{t-1}(a^2)^i = \frac{\sigma^2(1 - a^{2t})}{1 - a^2}. \end{align}
When we choose $a = \sqrt{1 - \sigma^2}$ we obtain $\sigma^2 = 1 - a^2$ and henceforth
$$q(x_t| x_0) = \N(a^t x_{0}, 1 - a^{2t}).$$
Obviously, for large $t$, the flow converges to an isotropic Gaussian:
$$q(x_t|x_0) \rightarrow \N(0, 1).$$
1.1.2. Diffusion with varying update factors¶
Next, we look into the case where the update factor depends on time. Let's add Gaussian noise to the data according to a variance schedule $\beta_1, \ldots, \beta_T$:
\begin{align} x_0 & \sim \pi(x_0) \\ t & = 1,2,\dots \\ x_t & = \sqrt{1-\beta_t} x_{t-1} + \sqrt{\beta_t} \epsilon_t. \end{align}
Notice that $\beta_t: 0 → 1$ interpolates between a constant Markov chain to white noise. For notational convenience, we define
\begin{align} \alpha_t &= 1 - \beta_t \quad \text{and} \quad \bar{\alpha}_t = \prod_{i=1}^t \alpha_i. \end{align}
We have
\begin{align} x_1 & = \sqrt{\alpha_1} x_{0} + \sqrt{1 - \alpha_1} \epsilon_1 \\ x_2 & = \sqrt{\alpha_2} (\sqrt{\alpha_1} x_{0} + \sqrt{1 - \alpha_1} \epsilon_1) + \sqrt{1 - \alpha_2} \epsilon_2 = \sqrt{\bar{\alpha}_2} x_{0} + \sqrt{\alpha_2} \sqrt{1 - \alpha_1} \epsilon_1 + \sqrt{1 - \alpha_2}\epsilon_2\\ x_3 & = \sqrt{\bar{\alpha}_3} x_{0} + \sqrt{\alpha_3}\sqrt{\alpha_2} \sqrt{1 - \alpha_1} \epsilon_1 + \sqrt{\alpha_3} \sqrt{1 - \alpha_2}\epsilon_2 + \sqrt{1 - \alpha_3}\epsilon_3\\ \dots \\ x_t & = \sqrt{\bar{\alpha}_t} x_{0} + \frac{\sqrt{\bar{\alpha}_t}}{\sqrt{\bar{\alpha}_1}} \sqrt{1 - \alpha_1} \epsilon_1 + \frac{\sqrt{\bar{\alpha}_t}}{\sqrt{\bar{\alpha}_2}} \sqrt{1 - \alpha_2} \epsilon_2 + \dots + \frac{\sqrt{\bar{\alpha}_t}}{\sqrt{\bar{\alpha}_{t-1}}} \sqrt{1 - \alpha_{t-1}} \epsilon_{t-1} + \sqrt{1 - \alpha_{t}} \epsilon_{t} \\ & = \sqrt{\bar{\alpha}_t} x_{0} + \sqrt{\bar{\alpha}_t} \left(\sqrt{\frac{1 - \alpha_1}{\bar{\alpha}_1} } \epsilon_1 + \sqrt{\frac{1 - \alpha_2}{\bar{\alpha}_2}} \epsilon_2 + \dots + \sqrt{\frac{1 - \alpha_{t-1}}{\bar{\alpha}_{t-1}}} \epsilon_{t-1} + \sqrt{\frac{1 - \alpha_{t}}{\bar{\alpha}_{t}}} \epsilon_{t} \right). \end{align}
As above, the expectation of a future state $x_t$ conditioned on the initial state $x_0$ has a simple form:
$$\E{x_t| x_0} = \sqrt{\bar{\alpha}_t} x_{0}.$$
Then we look at the variance of $x_t$.
\begin{align} \E{(x_t - \E{x_t|x_0})^2} & = {\bar{\alpha}_t} \left({\frac{1 - \alpha_1}{\bar{\alpha}_1} } + {\frac{1 - \alpha_2}{\bar{\alpha}_2}} + {\frac{1 - \alpha_3}{\bar{\alpha}_3}} + \dots + {\frac{1 - \alpha_{t-1}}{\bar{\alpha}_{t-1}}} + {\frac{1 - \alpha_{t}}{\bar{\alpha}_{t}}} \right) \\ & = {\bar{\alpha}_t} \left({\frac{\alpha_2 - \alpha_1 \alpha_2}{\bar{\alpha}_1 \alpha_2} } + {\frac{1 - \alpha_2}{\bar{\alpha}_2}} + {\frac{1 - \alpha_3}{\bar{\alpha}_3}} + \dots + {\frac{1 - \alpha_{t-1}}{\bar{\alpha}_{t-1}}} + {\frac{1 - \alpha_{t}}{\bar{\alpha}_{t}}} \right), \quad \text{note}~ \bar{\alpha}_{t} = \alpha_t \bar{\alpha}_{t-1} \\ & = {\bar{\alpha}_t} \left({\frac{1 - \alpha_1 \alpha_2}{\bar{\alpha}_2}} + {\frac{1 - \alpha_3}{\bar{\alpha}_3}} + \dots + {\frac{1 - \alpha_{t-1}}{\bar{\alpha}_{t-1}}} + {\frac{1 - \alpha_{t}}{\bar{\alpha}_{t}}} \right) \\ & = {\bar{\alpha}_t} \left({\frac{1 - \bar{\alpha}_3}{\bar{\alpha}_3}} + \dots + {\frac{1 - \alpha_{t-1}}{\bar{\alpha}_{t-1}}} + {\frac{1 - \alpha_{t}}{\bar{\alpha}_{t}}} \right) = 1 - \bar{\alpha}_t \\ & = {\bar{\alpha}_t} \left( {\frac{1 - \bar{\alpha}_{t}}{\bar{\alpha}_{t}}} \right) = 1 - \bar{\alpha}_t. \end{align}
Consequently we obtain the following distribution for future states $x_t$:
$$q(x_t|x_0) = \N(x_t; \sqrt{\bar{\alpha}_t} x_{0}, 1 - \bar{\alpha}_t).$$
Notice that our previous observation ($\beta_t: 0 → 1$ interpolates between a constant Markov chain to white noise) still holds as $\beta_t: 0 → 1$ implies $\alpha_t: 1 → 0$.
1.1.3. An example diffusion¶
In the following example, we have a very simple dataset with 4 data points:
$$ \mathcal{D} = \{-15, -5, 1, 10\}.$$
Flow demonstration¶
Now we check that $q_t(x_t)$ looks like. Below, we visualize $q_t(x_t)$ over time $t$. For each initial value (the dataset), we simulate the Markov chain 25 times. Also, notice that since we have 4 initial values (data points), $q_t(x_t)$ is a Gaussian mixture with 4 components.
mu_0 = torch.tensor([-15, 1, -5, 15],dtype=dtype,device=device)
def sample_prior(num_samples, sig_pri=0):
idx = torch.randint(mu_0.shape[0],[num_samples])
x = mu_0[idx]
samples = x + sig_pri * torch.randn_like(x)
return samples
N = 100 # Number of samples
T = 200 # Number of time steps
sig = 0.2 # reverse process noise
betas = torch.ones(T,dtype=dtype,device=device) * sig**2 # fixed noise parameter
alphas = 1 - betas # see above definitions <---> a^2+b=1
alpha_bars = alphas.cumprod(0)
# particles to be flown
Xf = torch.zeros(N, T, dtype=dtype,device=device)
Xf[:, 0] = sample_prior(N)
# run the chain forward
for t in range(T-1):
Xf[:, t+1] = np.sqrt(1-betas[t]) * Xf[:, t] + np.sqrt(betas[t])*np.random.randn(N)
# visualize
plt.figure(1,(12,6))
p1 = plt.plot(Xf.T, 'tab:blue', alpha=0.1, label='all particles')
std = Xf.std(0)
m = Xf.mean(0)
p2 = plt.plot(m, '--', color='tab:red', lw=3, label='$\mu \pm 3*\sigma$')
plt.plot(m + 3*std, '--', color='tab:red', lw=1)
plt.plot(m - 3*std, '--', color='tab:red', lw=1)
p3 = plt.plot(Xf[0:2, :].T, 'tab:olive', label='two particles')
plt.xlabel('t')
plt.legend(handles=[p1[0],p2[0],p3[0]], fontsize=15)
plt.grid()
plt.show()
Time marginals - how to compute marginal densities $q_t(x_t)$ over time¶
# time marginals
def gaussian_pdf(x, mu, sig2):
if sig2 == 0:
sig2 = 1e-5
return torch.exp(-0.5*(x - mu)**2/sig2) / np.sqrt(2*np.pi*sig2)
# computes the density q_t at time t given initial value(s) x_0
def marginal(x_0, a_bar_t):
mu = np.sqrt(a_bar_t) * x_0
v = (1-a_bar_t) * torch.ones_like(mu)
return mu, v
def eval_mixture_density(mu, v, x_grid):
''' Evaluates the density of each x in x_grid under N Gaussian mixtures
mu - [N]
var - [N]
x_grid - [M]
'''
if v[0] == 0:
v += 1e-10
N,M = len(mu),len(x_grid)
x_grid = torch.stack([x_grid]*N) # N,M
v,mu = v.reshape(N,1), mu.reshape(N,1)
dens = torch.exp(-0.5*(x_grid - mu)**2/v) / (2*np.pi*v).sqrt() # N,M
return dens.mean(0)
x_grid = torch.linspace(-16, 16, 3201)
q_ts = torch.zeros(T,len(x_grid))
marg_mus = torch.zeros(T,N,dtype=dtype,device=device)
marg_vars = torch.zeros(T,N,dtype=dtype,device=device)
for t in range(T):
marg_mus[t], marg_vars[t] = marginal(Xf[:, 0], alpha_bars[t]) # one Gausssian per particle
q_ts[t] = eval_mixture_density(marg_mus[t], marg_vars[t], x_grid) # Ngrid
Density animation - a histogram of simulated particles $q_t(x_t)$ (mixture of Gaussian)¶
PLOT_EVERY = T//100
fig, ax = plt.subplots()
ax.set_title(f'time = {0}')
ax.set_xlabel(r'x_t',fontsize=14)
ax.set_xlabel(r'q_t(x_t)',fontsize=14)
def animate(t):
ax.cla()
t_plot = t*PLOT_EVERY
ax.set_title(f'time = {t_plot}')
ax.hist(Xf[:, t_plot].cpu().numpy(), 10, density=True, alpha=0.4)
ax.plot(x_grid, q_ts[t_plot])
if t>0:
ax.set_ylim([0, 0.5])
ax.set_xlabel(r'$x_t$',fontsize=14)
ax.set_ylabel(r'$q_t(x_t)$',fontsize=14)
return ax
anim = FuncAnimation(fig, animate, frames=T//PLOT_EVERY, interval=50)
anim.save('anims/1forward_histogram.gif', writer=PillowWriter(fps=20))
plt.close()
HTML(anim.to_jshtml())
Marginal density contourplot¶
PLOT_EVERY = T//50
real_x = np.arange(0,T)
real_y = x_grid
dx = (real_x[1]-real_x[0])/2.
dy = (real_y[1]-real_y[0])/2.
extent = [real_x[0]-dx, real_x[-1]+dx, real_y[-1]+dy, real_y[0]-dy]
fig, ax = plt.subplots(figsize=(16,9))
ax.imshow(q_ts[0:], extent=extent)
ax.imshow(q_ts[0:].T, extent=extent, aspect='auto', vmin=0.0, vmax=0.66)
parts = ax.plot(Xf[14:18, 0:1].T, 'tab:olive', label='two particles')
ax.set_xlabel('time',fontsize=20)
ax.set_ylabel('particles / density',fontsize=20)
ax.set_xlim([0,T])
# ax.colorbar()
def animate(t):
t_plot = t*PLOT_EVERY
# ax.plot(x[14:18, 0:t_plot].T, 'tab:olive', label='two particles')
for i,part in enumerate(parts):
part.set_xdata(np.arange(t_plot))
part.set_ydata(Xf[14+i, 0:t_plot])
plt.show()
plt.close()
anim = FuncAnimation(fig, animate, frames=T//PLOT_EVERY, interval=50)
anim.save('anims/2forward_flow.gif', writer=PillowWriter(fps=20))
HTML(anim.to_jshtml())
1.2. Inverting the forward diffusion¶
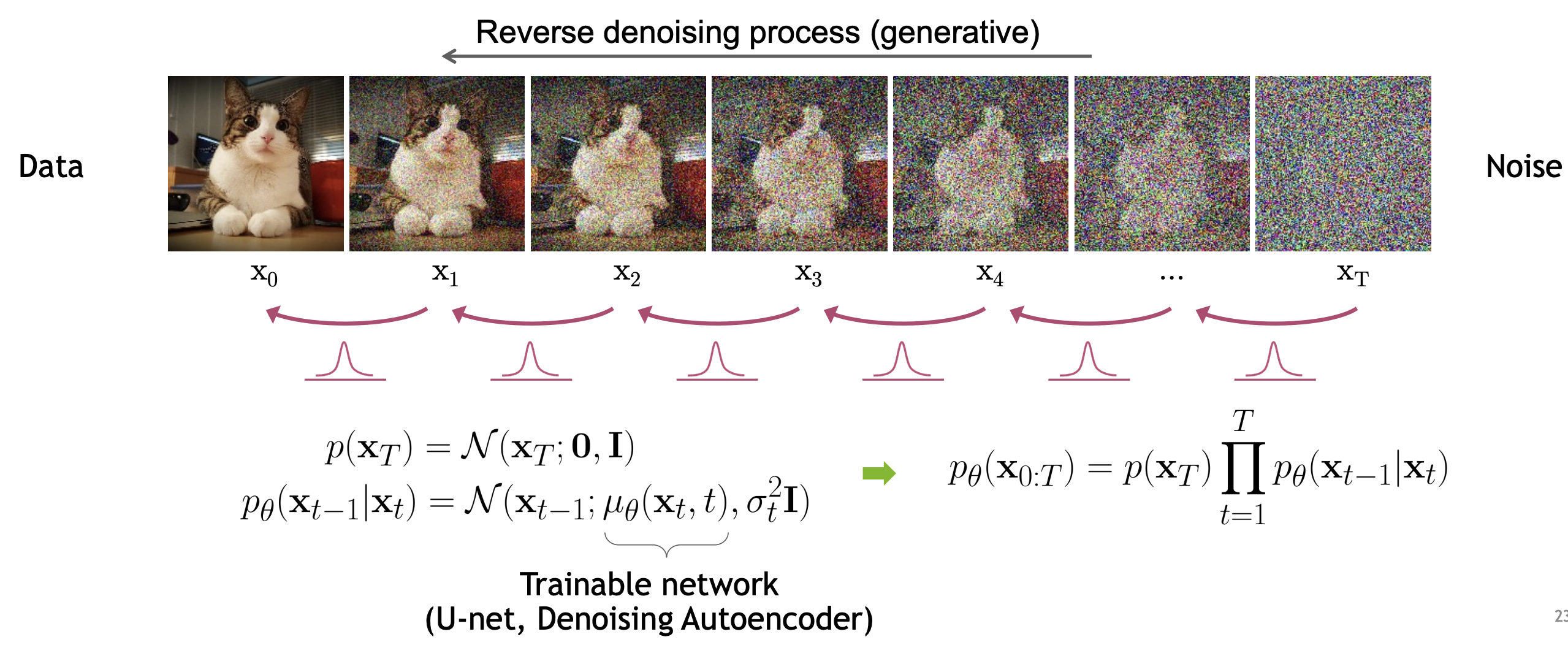
The key idea of a diffusion models is instead of directly sampling from $q(x_0)$, sampling from an alternative model $p(x_0)$ using a time reversed model $ p(x_T) p(x_{T-1}| x_T) \dots p(x_1| x_2) p(x_0|x_1)$ where $p(x_T) = \mathcal{N}(0, I)$.
\begin{align} p(x_{0:T}) = p(x_T) \prod_{t=2}^{T} p(x_{t-1} \mid x_{t}) \\ p(x_{t-1} \mid x_{t}) \triangleq p(x_{t-1} \mid \mu_\theta(x_{t},t)) \\ x_T & \sim \mathcal{N}(0, I) \\ t & = T-1,T-2,\dots, 1 \\ x_t & \sim p(x_{t}| x_{t+1}). \end{align}
1.2.1. The evidence lower bound¶
This derivation is based on the DDPM paper. As usual, for the empirical data distribution, $q(x_0)\equiv\pi(x_0)$ we would like to maximize the data log-likelihood
$$ \E[q(x_0)]{\log p(x_0)}. $$
We first write down a bound on the marginal log-likelihood
\begin{align} \log p(x_0) &= \log \int p(x_{0:T}) d x_{1:T} \\ &= \log \int p(x_{0:T}) \frac{q(x_{1:T})}{q(x_{1:T})} d x_{1:T} \\ &= \log \int q(x_{1:T}|x_0) \frac{p(x_{0:T})}{q(x_{1:T})} d x_{1:T} \\ &= \log \E[q(x_{1:T})]{\frac{p(x_{0:T})}{q(x_{1:T})}} \\ &\geq \E[q(x_{1:T})]{\log \frac{p(x_{0:T})}{q(x_{1:T})}} \\ &= \E[q(x_{1:T})]{\log \left( p(x_T) \prod_t \frac{p(x_{t-1}|x_t)}{q(x_t|x_{t-1})}} \right) \\ &= \E[q(x_T)]{\log p(x_T)} + \sum_t \E[q(x_{1:T})]{\frac{p(x_{t-1}|x_t)}{q(x_t|x_{t-1})}} \\ &= \E[q(x_T)]{\log p(x_T)} + \sum_t \E[q(x_{1:T})]{\frac{p(x_{t-1}|x_t)}{q(x_t|x_{t-1},x_0)}} \quad \text{// doable since forward process is Markovian} \\ &= \E[q(x_T)]{\log p(x_T)} + \sum_t \E[q(x_{1:T})]{\log \frac{p(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)\frac{q(x_t|x_0)}{q(x_{t-1}|x_0)} }} \quad \text{// to re-write in terms of KL divergences} \\ &= \E[q(x_T)]{\log p(x_T)} + \sum_t \E[q(x_{1:T})]{\log \frac{p(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}} \\ &= \E[q(x_T|x_0)]{\log p(x_T)} + \sum_t \E[q(x_{1:T}|x_0)]{\log \frac{p(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}} + \sum_t \E[q(x_{1:T}|x_0)]{\log \frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}} \\ &= \E[q(x_T|x_0)]{\log p(x_T)} - \sum_t \text{KL}\left[q(x_{t-1}|x_t,x_0) \| p(x_{t-1}|x_t) \right] + \E[q(x_1|x_0)]{\log q(x_1|x_0)} - \E[q(x_T|x_0)]{\log q(x_T|x_0)}. \end{align}
Maximizing the lower bound imply minimizing the KL divergence. In other words, the backward model $p(x_{t-1}|x_t)$ approximates the posterior $q(x_{t-1}|x_t,x_0)$ of the forward model. We first write down the posterior:
\begin{align} q(x_{t-1}|x_t,x_0) &= \N(x_{t-1};\bar{\mu}(x_t,x_0),\bar{\beta}_t) \\ \bar{\mu}(x_t,x_0) &= \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t \\ \bar{\beta}_t &= \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_t. \end{align}
To minimize the KL, the mean of the backward flow $\mu_\theta(x_t,t)$ should match the above mean:
\begin{align} \min_\theta ~~ \E[x_0,\epsilon] {\frac{1}{2\sigma_t^2} \Bigg\| \bar{\mu}(x_t,x_0) - \mu_\theta(x_t,t) \Bigg\|}. \end{align}
Next, we plug in the forward state
$$ x_t = \sqrt{\bar{\alpha}_t} x_{0} + \epsilon (1 - \bar{\alpha}_t), \quad \epsilon \sim \N(0,1), $$
which gives
\begin{align} \min_\theta ~~ & \E[x_0,\epsilon]{\frac{1}{2\sigma_t^2} \Bigg\| \bar{\mu}\left(x_t, \frac{x_t - \epsilon (1 - \bar{\alpha}_t)}{\sqrt{\bar{\alpha}_t} } \right) - \mu_\theta(x_t,t) \Bigg\|} \\ \min_\theta ~~ & \E[x_0,\epsilon]{\frac{1}{2\sigma_t^2} \Bigg\| \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon \right) - \mu_\theta(x_t,t) \Bigg\|}. \end{align}
That means, the mean function $\mu_\theta(x_t,t)$ should predict a function of known terms, $x_t$ and also noise $\epsilon$. This is why it performs denoising. After re-parameterizing above loss, the optimization objective and the generative process become the following:

Learning $\epsilon_\theta$¶
x0 = Xf[:,:1] # data points
N,d = x0.shape # data shape
Nmini = 100 # batch size
Niter = 5000 # number of optimization iterations
H = 256
denoiser = nn.Sequential(
nn.Linear(d+1,H),
nn.ELU(),
nn.Linear(H,H),
nn.ELU(),
nn.Linear(H,H),
nn.ELU(),
nn.Linear(H,H),
nn.ELU(),
nn.Linear(H,d)
)
# load the model
denoiser.load_state_dict(torch.load('trained_denoiser.pt'))
# or train it
# opt = torch.optim.Adam(denoiser.parameters(), 1e-4)
# for i in range(Niter):
# opt.zero_grad()
# # pick a subset of data
# rand_idx = torch.randperm(N)[:Nmini]
# x0_i = x0[rand_idx] # Nmini,d
# # sample the noise
# eps = torch.randn_like(x0_i) # Nmini,d
# # pick random time points
# T_i = torch.randperm(T)[:Nmini].unsqueeze(-1) # Nmini,d
# # prepare input to the denoiser network
# alpha_bar_i = alpha_bars[T_i] # Nmini,d
# xt_i = x0_i*np.sqrt(alpha_bar_i) + np.sqrt(1-alpha_bar_i)*eps # Nmini,d
# inp = torch.cat([xt_i,T_i],-1) # Nmini,d+1
# # compute the loss
# loss = (eps-denoiser(inp)).pow(2).mean()
# loss.backward()
# opt.step()
# if i%(Niter//20)==0:
# print('iter={:<4d}, loss={:.3f}'.format(i,loss.item()))
<All keys matched successfully>
Generation: simulating backward in time (Algorithm 2)¶
# backward flow
N = 100 # num. simulated particles
d = 1 # data dim
x0 = torch.randn(N,d)
Xb = torch.zeros(T,N,d)
Xb[-1] = x0
with torch.no_grad():
for t in range(T-1,0,-1):
z = torch.randn_like(Xb[t])
inp = torch.cat([Xb[t],t*torch.ones(N,1)],-1) # N,d+1
denoising_term = denoiser(inp) # N,d+1
fac = (1-alphas[t])/(math.sqrt(1-alpha_bars[t]))
Xb[t-1] = ( Xb[t] - fac*denoising_term ) / np.sqrt(alphas[t]) + z*sig
plt.figure(1,(12,6))
plt.plot(Xb.squeeze(-1))
plt.title('Backward flow via the learned noise estimator',fontsize=18);
fig, ax = plt.subplots(figsize=(16,9))
PLOT_EVERY = 4
def animate(t):
ax.cla()
t_end = T-1
t_beg = T-1-t*PLOT_EVERY
ax.plot(np.arange(t_beg,t_end), Xb[t_beg:t_end,:,0],'-')
ax.set_xlim([0,T])
ax.set_ylim([Xb.min()-1,Xb.max()+1])
ax.set_title(f't={t*PLOT_EVERY} - Backward flow via the learned noise estimator',fontsize=18);
anim = FuncAnimation(fig, animate, frames=T//PLOT_EVERY, interval=50)
anim.save('anims/3backward_learned.gif', writer=PillowWriter(fps=20))
plt.close()
HTML(anim.to_jshtml())