Lecture notes and code samples from ML Foundations Summer School in Bilimler Koyu. The notebook is based largely on the following resources:
The text is generated by ChatGPT - after careful prompting 😋
Import statements¶
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
from torch.nn.utils.rnn import pad_sequence
from torchvision.datasets import CIFAR10
from torchvision import transforms
import numpy as np
import matplotlib.pyplot as plt
from datasets import load_dataset
from transformers import AutoTokenizer
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
/mnt/lustre/work/vernade/cyildiz40/.conda/sumsch/lib/python3.11/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html from .autonotebook import tqdm as notebook_tqdm
The main task in this notebook¶
We will learn a higher-order Markovian model that
- takes as input some context that has length more than 1
- predicts the future based on the context: \begin{align*} p(x_0, x_1, \ldots, x_N) = p(x_0) \prod_{n=1}^N p(x_n | x_{<n}) \end{align*}
This model will translate German to English. Let's see what the dataset looks like.
tok = AutoTokenizer.from_pretrained("Helsinki-NLP/opus-mt-de-en")
if tok.bos_token is None:
tok.add_special_tokens({"bos_token": "<bos>"})
if tok.pad_token is None:
tok.add_special_tokens({"pad_token": "<pad>"})
if tok.eos_token is None:
tok.add_special_tokens({"eos_token": "<eos>"})
print('Vocab size:', len(tok))
ds_train = load_dataset("bentrevett/multi30k", split="train") # fields: "de", "en"
ds_valid = load_dataset("bentrevett/multi30k", split="validation")
# Peek at the first example
print(len(ds_train), 'data points.')
print('\nAn example data point:', ds_train[0])
de_en = '[DE] ' + ds_train[0]['de'] + ' [EN] ' + ds_train[0]['en']
print('\nInput-outputs derived from the first data point:')
split_de_en = de_en.split(' ')
for i in range(14,23):
print('\nInput:', ' '.join(split_de_en[:i]))
print('Output:', ' '.join(split_de_en[i:i+1]))
# print('\nInput:', de_en[:76])
# print('Output:', de_en[76:79])
# print('\nInput:', de_en[:80])
# print('Output:', de_en[80:85])
# print('\nInput:', de_en[:87])
# print('Output:', de_en[87:92])
# print('\nInput:', de_en[:93])
/mnt/lustre/work/vernade/cyildiz40/.conda/sumsch/lib/python3.11/site-packages/transformers/models/marian/tokenization_marian.py:175: UserWarning: Recommended: pip install sacremoses.
warnings.warn("Recommended: pip install sacremoses.")
Vocab size: 58102
29000 data points.
An example data point: {'en': 'Two young, White males are outside near many bushes.', 'de': 'Zwei junge weiße Männer sind im Freien in der Nähe vieler Büsche.'}
Input-outputs derived from the first data point:
Input: [DE] Zwei junge weiße Männer sind im Freien in der Nähe vieler Büsche. [EN]
Output: Two
Input: [DE] Zwei junge weiße Männer sind im Freien in der Nähe vieler Büsche. [EN] Two
Output: young,
Input: [DE] Zwei junge weiße Männer sind im Freien in der Nähe vieler Büsche. [EN] Two young,
Output: White
Input: [DE] Zwei junge weiße Männer sind im Freien in der Nähe vieler Büsche. [EN] Two young, White
Output: males
Input: [DE] Zwei junge weiße Männer sind im Freien in der Nähe vieler Büsche. [EN] Two young, White males
Output: are
Input: [DE] Zwei junge weiße Männer sind im Freien in der Nähe vieler Büsche. [EN] Two young, White males are
Output: outside
Input: [DE] Zwei junge weiße Männer sind im Freien in der Nähe vieler Büsche. [EN] Two young, White males are outside
Output: near
Input: [DE] Zwei junge weiße Männer sind im Freien in der Nähe vieler Büsche. [EN] Two young, White males are outside near
Output: many
Input: [DE] Zwei junge weiße Männer sind im Freien in der Nähe vieler Büsche. [EN] Two young, White males are outside near many
Output: bushes.
1. Introduction¶
Different architectures¶
Over the past decades, machine learning has produced many different architectures, each suited to different kinds of data:
- Multilayer perceptrons (MLPs) were the earliest general-purpose neural networks, used for tasks like basic classification and regression.
- Convolutional neural networks (CNNs) then became the workhorse for computer vision, learning how to recognize patterns in images by exploiting local structure.
- For sequential data, recurrent neural networks (RNNs) were widely adopted, because they could process variable-length sequences by maintaining a hidden state over time. A prominent example of RNNs in practice was machine translation, where models such as the Sequence-to-Sequence architecture (Sutskever et al., 2014, figure below) with attention mechanisms (Bahdanau et al., 2015) achieved major breakthroughs.
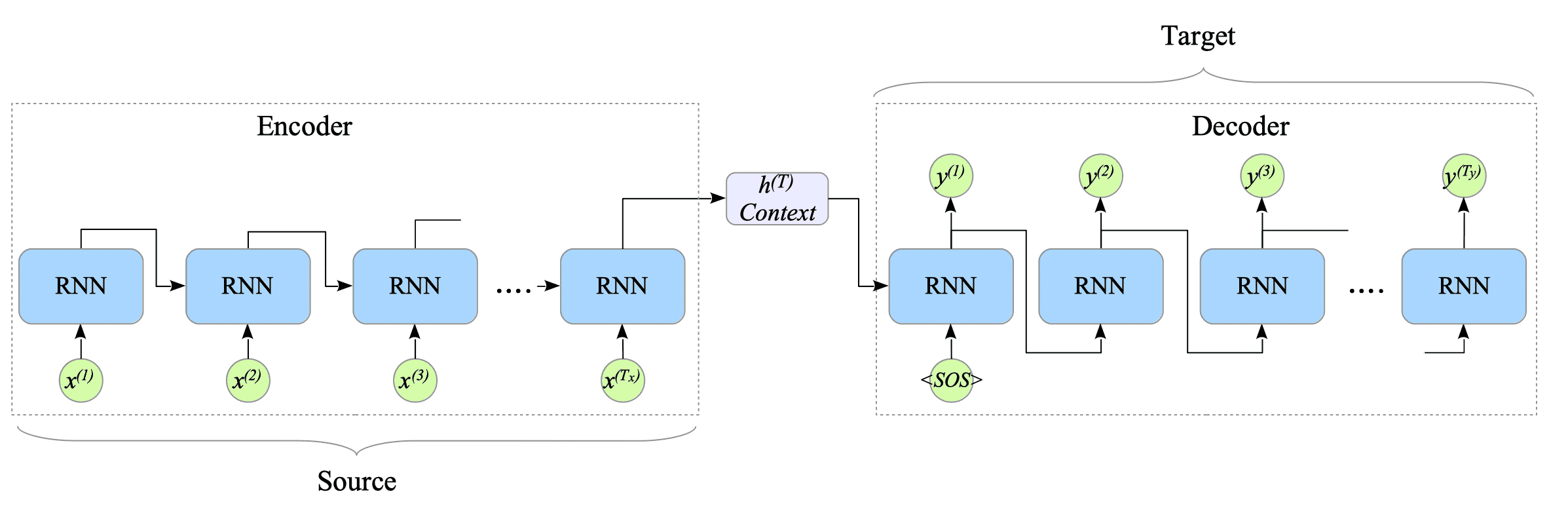
A cartoon illustration of RNN-based machine translation (image from https://www.interdb.jp/dl/part03/ch13.html)
Attention¶
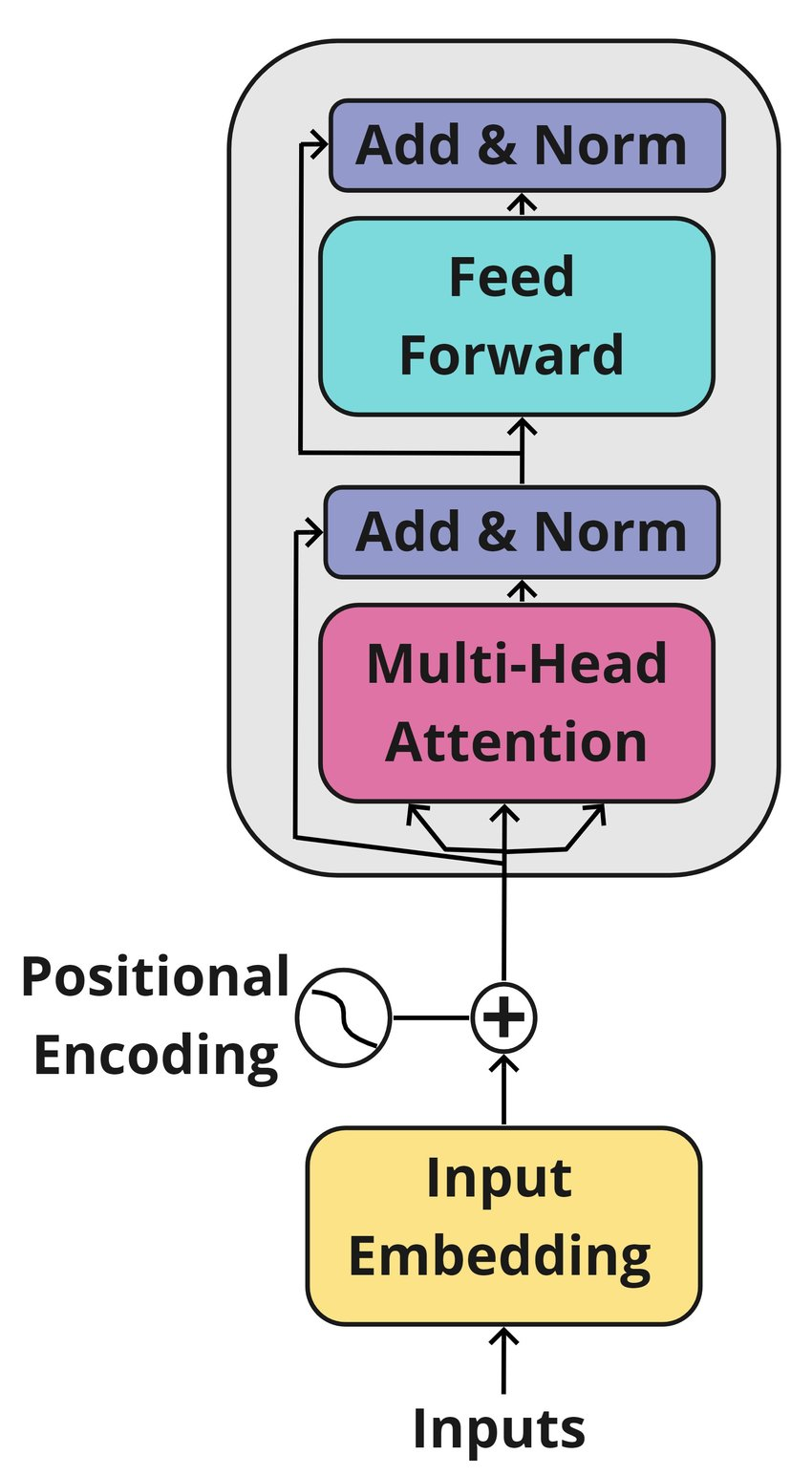
The idea of attention itself was revolutionary. It allowed models to dynamically focus on the most relevant parts of the input, instead of compressing everything into a single fixed-size vector. Early applications included neural machine translation, image captioning, and speech recognition. But then came a turning point: the landmark paper “Attention Is All You Need” (Vaswani et al., 2017). This work proposed the Transformer, a model built entirely around attention layers, without recurrence or convolutions. It introduced the now-famous encoder–decoder architecture, where the encoder transforms an input sequence (like a German sentence) into a sequence of contextual representations, and the decoder generates the output sequence (like the English translation) step by step, attending both to the encoder’s outputs and to its own past predictions.
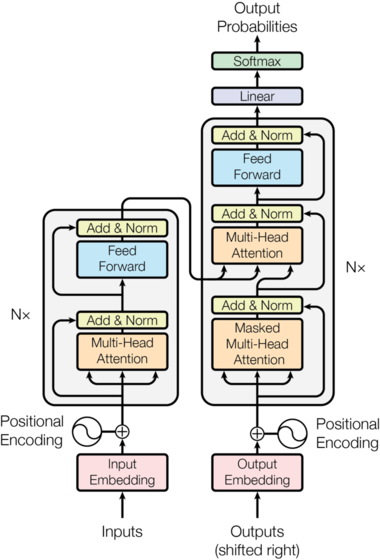
Attention is all you need architecture (image from Vaswani et al., 2017)
Causal language models¶
The Transformer quickly became the dominant architecture for language tasks, and soon spread to vision, speech, and beyond. But in this tutorial, our focus will not be on faithfully reproducing the exact “Attention Is All You Need” setup. Instead, we’ll study the core building blocks — attention, masking, autoregression — through the lens of causal language models (LLMs). These models, like GPT-2 (Radford et al., 2019) and its descendants, use the Transformer in a simpler “decoder-only” form, where the goal is always the same: predict the next token given the previous ones. By starting here, we’ll build a clear intuition for how modern translation and large-scale language models are trained.
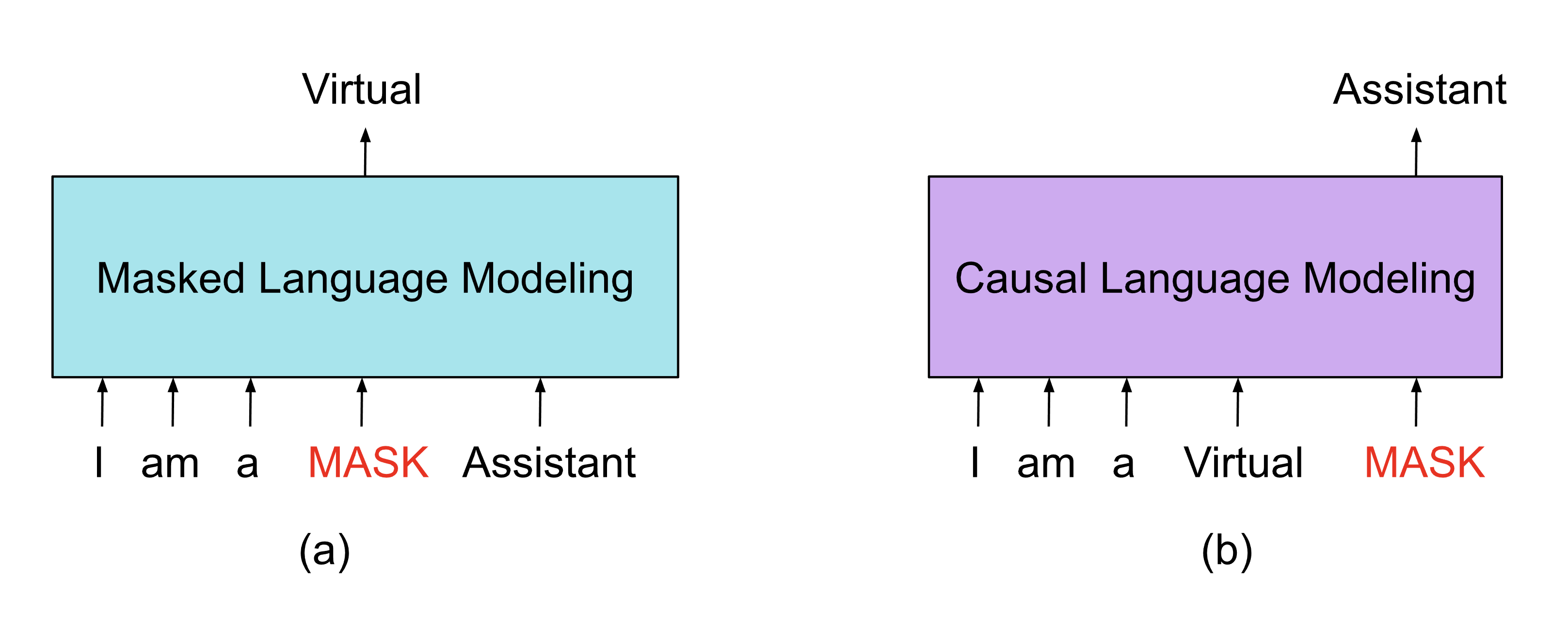
Causal vs masked language models (image from https://www.holisticai.com/blog/from-transformer-architecture-to-prompt-engineering)
What are we going to implement?¶
1. A Transformer network¶
We will implement, from scratch, a transformer network. This network will be quite generic - so much so that it could be used even for computer vision as we demonstrate at the end of this notebook.
2. Auto-regressive (causal) next item predictors¶
A central idea in sequence modeling is auto-regression: given a sequence of items, a model learns to predict the next item based on the context of all previous ones. Here, the model could be any ML model, and we will consider MLPs and Transformers. This approach is powerful because it transforms the problem of modeling complex sequences into a series of simple, repeated predictions. For text, this means predicting the next word given the words that came before; for time series, it could mean predicting tomorrow’s value from past values. Once trained, such a model can be used to generate arbitrarily long sequences: start with an initial context, predict the next token, append it to the context, and repeat. This is the principle behind modern large language models like GPT.
3. Data loaders and training modules¶
Of course, we would like to see if our method actually works or not. For this, we will consider a German-to-English translation dataset
T = 256 # Context length (sequence length)
V = 10000 # Vocabulary size (for embeddings)
N = 12 # Number of Transformer blocks
d = 256 # Embedding dimension
H = 8 # Number of attention heads
class TransformerNetwork(nn.Module):
def __init__(self, T, N, input_emb, pos_emb, transf_block, norm_layer, output_layer):
''' Transformer network with N blocks, context length T, and given components.
Args:
T: Context length (sequence length).
N: Number of Transformer blocks.
input_emb: Input embedding layer/module.
pos_emb: Positional embedding layer/module.
transf_block: A single Transformer block (to be repeated N times).
norm_layer: Normalization layer/module (e.g., LayerNorm).
output_layer: Output layer/module (e.g., for classification or regression).
'''
super(TransformerNetwork, self).__init__()
self.T = T
self.input_emb = input_emb
self.pos_emb = pos_emb
self.transf_blocks = nn.ModuleList([transf_block for _ in range(N)])
self.norm_layer = norm_layer
self.output_layer = output_layer
@property
def device(self):
return next(self.parameters()).device
@property
def dtype(self):
return next(self.parameters()).dtype
@property
def num_layers(self):
return len(self.transf_blocks)
@property
def d(self):
return self.input_emb.embedding_dim
def forward(self, X):
'''
Forward pass through the Transformer network.
Args:
X: Input tensor of shape (batch_size, T, input_dim), or (B,T,d).
Returns:
Output tensor after passing through the Transformer network.
'''
device = X.device
B,T = X.shape[0:2]
# assert T == self.T, f'Input sequence length {T} does not match model context length {self.T}.'
# Input embedding
X = self.input_emb(X) # B,T,d
# positional embeddings
P = self.pos_emb(torch.arange(T, device=device)) # T,d
P = P.unsqueeze(0).expand(B, T, -1) # B,T,d
# adding positional embeddings
X = X + P # B,T,d
# passing through Transformer blocks
for block in self.transf_blocks:
X = block(X) # B,T,d
# final normalization
X = self.norm_layer(X) # B,T,d
# output layer
out = self.output_layer(X) # B,T,output_dim (depends on output_layer)
return out
2.2. Embeddings and positional encodings¶
At the input layer, tokens are first mapped into embeddings, and we add positional encodings so the model can take the token order into account. The sequence of embeddings is then passed through a stack of Transformer blocks:
- Embeddings: Neural networks cannot work directly with discrete symbols (like words or image patches), so we map them into continuous vectors called embeddings. These vectors capture semantic or structural properties in a way that the model can process. In NLP, embeddings represent tokens such that similar words are close in vector space; in vision, embeddings represent image patches or regions in a comparable way.
- Positional encodings: Transformers do not have an inherent sense of order, since self-attention treats all tokens symmetrically. To provide the model with information about sequence or spatial position, we add positional encodings to the embeddings. In text, this means encoding word positions within a sentence; in vision, it means encoding the 2D location of a patch within an image. These positional signals let the model distinguish, for example, “the first word in a sentence” or “a patch in the top-left corner of an image.”
def create_embedding(input_dim, output_dim):
''' Creates an embedding layer for input tokens. '''
return nn.Embedding(input_dim, output_dim)
input_emb = create_embedding(V, d) # Input embedding
pos_emb = create_embedding(T, d) # Positional embedding
# example usage of positiona embeddings
P = pos_emb(torch.arange(T)) # Example usage to get positional embeddings for positions 0 to T-1
plt.figure(figsize=(8,4))
plt.imshow(P.detach().cpu().numpy(), aspect='auto')
plt.colorbar()
plt.title('Positional Embeddings (not trained yet)')
plt.xlabel('Embedding Dimension')
plt.ylabel('Position')
plt.show()
2.3. Transformer blocks¶
Each Transformer block has two main components:
- Multi-Head Self-Attention (MHSA), which allows every token to attend to other tokens in the sequence, gathering relevant context.
- Feed-Forward Network (FFN), a small MLP applied to each token representation independently.
Both parts are wrapped with residual connections and layer normalization for stable training.
- Layer normalization works by normalizing the activations of each token representation across its hidden dimensions, ensuring that values have consistent scale and distribution. This helps gradients flow more reliably, reduces sensitivity to initialization, and allows the model to train deeper networks without diverging. In practice, it is usually applied together with residual connections, so that the model learns new information while preserving the original signal.
class Block(nn.Module):
def __init__(self, mhsa, d, d_ff, dropout=0.1):
''' A single Transformer block with Multi-Head Self-Attention and Feed-Forward Network.
Args:
mhsa: Multi-Head Self-Attention module.
d: Embedding dimension.
d_ff: Dimension of the feed-forward network.
dropout: Dropout rate.
'''
super(Block, self).__init__()
self.mhsa = mhsa
self.ffn = nn.Sequential(
nn.Linear(d, d_ff),
nn.ReLU(),
nn.Linear(d_ff, d)
)
self.norm1 = nn.LayerNorm(d)
self.norm2 = nn.LayerNorm(d)
self.dropout = nn.Dropout(dropout)
def forward(self, X):
'''
Forward pass through the Transformer block.
Args:
X: Input tensor of shape (B, T, d).
Returns:
Output tensor of shape (B, T, d).
'''
X = X + self.dropout(self.mhsa(self.norm1(X)))
X = X + self.dropout(self.ffn(self.norm2(X)))
return X
2.4. Self-attention implementation¶
Within attention, the terms query, key, and value have special meaning:
- A query vector represents the current token asking “what information do I need?”
- Key vectors represent all tokens as potential “addresses” to look up.
- Value vectors hold the actual information to be passed along.
Attention works by comparing queries against keys (using dot products), producing weights that determine how strongly each token’s value contributes to the output. This mechanism lets the model learn what to pay attention to at every step.
For an input $X = x_{1:n}$, where each token $x \in \mathbb{R}^d$, we first obtain queries, keys and values:
\begin{align} Q &= W_q^\top X \in \mathbb{R}^{n\times d_q}\\ K &= W_k^\top X \in \mathbb{R}^{n\times d_q}\\ V &= W_v^\top X \in \mathbb{R}^{n\times d_v}\\ \end{align}
For each query $\{q_i\} \in \mathbb{R}^{d_q}$, we compute its similarity to a key with \begin{align*} \text{sim}(q_i,k_j) \sim \exp(q_i^\top k_j) \end{align*} Then we normalize this across all values, which is implemented as $\texttt{softmax}$ below: \begin{align*} \text{sim}(q_i,k_j) = \frac{ \exp(q_i^\top k_j) } {\sum_m \exp(q_i^\top k_m) } \end{align*} The final output is a weighted average of values: \begin{align*} z_i = \sum_j \text{sim}(q_i,k_j) v_j \end{align*}
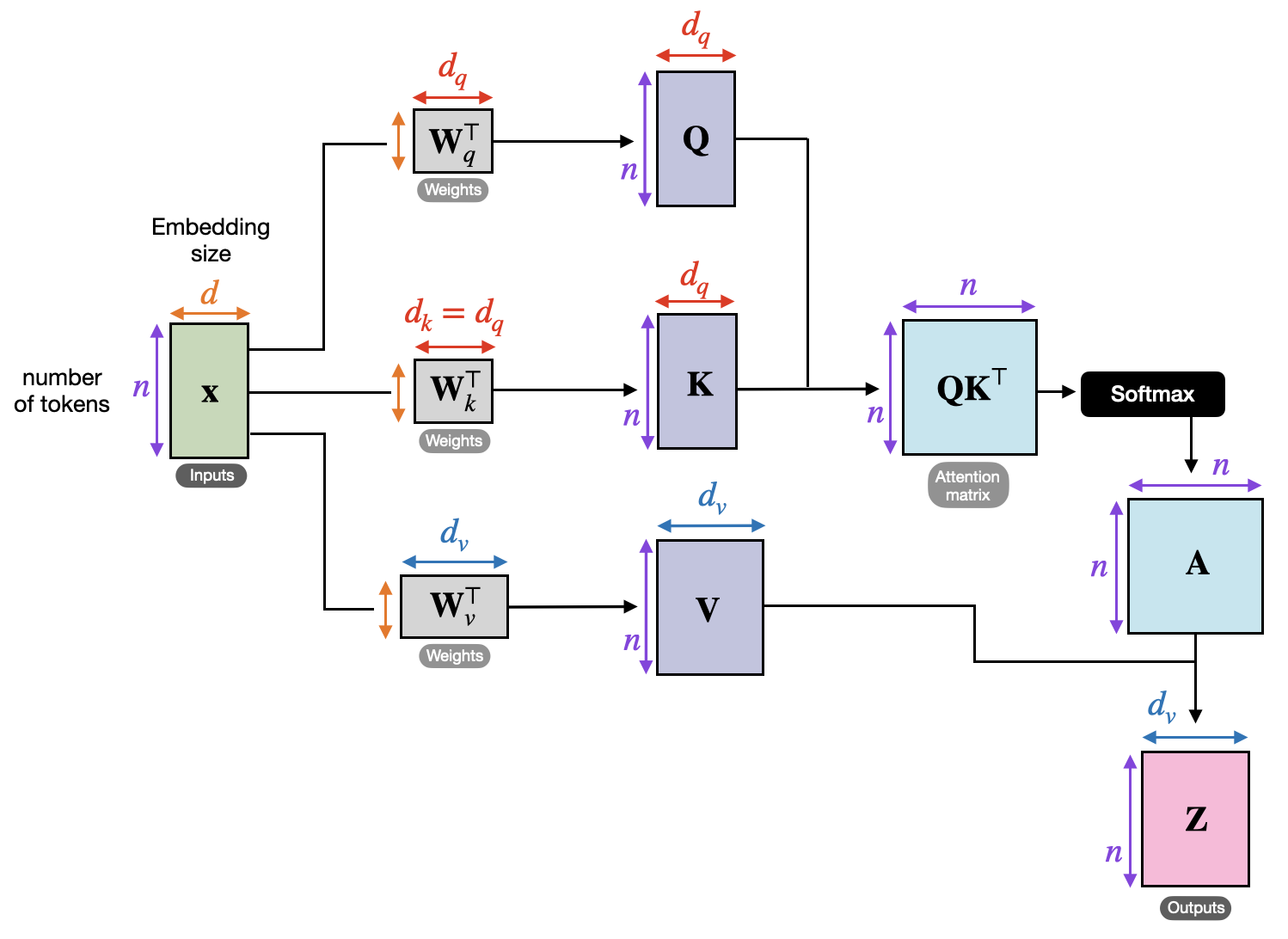
Self-attention calculations (image from https://sebastianraschka.com/blog/2023/self-attention-from-scratch.html)
class MultiHeadSelfAttention(nn.Module):
def __init__(self, d, H):
''' Multi-Head Self-Attention module.
Args:
d: Embedding dimension.
H: Number of attention heads.
'''
super(MultiHeadSelfAttention, self).__init__()
assert d % H == 0, "Embedding dimension must be divisible by number of heads."
self.d = d
self.H = H
self.d_k = d // H # Dimension per head
self.qkv = nn.Linear(d, 3*d) # Combined query, key, value projection
self.out = nn.Linear(d, d) # Output projection
def forward(self, X):
'''
Forward pass through the Multi-Head Self-Attention module.
Args:
X: Input tensor of shape (B, T, d).
Returns:
Output tensor of shape (B, T, d).
'''
B, T, d = X.shape
assert d == self.d, f'Input embedding dimension {d} does not match model dimension {self.d}.'
# Linear projections
qkv = self.qkv(X)
q,k,v = qkv.chunk(3, dim=-1) # Each is (B, T, d) ---> form queries, keys, values
# split into heads
q_reshaped = q.view(B, T, self.H, self.d_k).transpose(1,2) # (B, H, T, d_k)
k_reshaped = k.view(B, T, self.H, self.d_k).transpose(1,2) # (B, H, T, d_k)
v_reshaped = v.view(B, T, self.H, self.d_k).transpose(1,2) # (B, H, T, d_k)
# Scaled dot-product attention
k_transpose = k_reshaped.transpose(-2, -1) # (B, H, d_k, T)
QK = q_reshaped @ k_transpose # (B, H, T, T) ---> QK[b,h,i] stores the similarity of token i to all tokens in the sequence
attn = QK.softmax(dim=-1) # (B, H, T, T) ---> attn[b,h,i] stores how much token i attends to all tokens in the sequence
# alternative computation of softmax
# alt_computation = QK.exp() / QK.exp().sum(dim=-1, keepdim=True)
# assert torch.allclose(attn, alt_computation, atol=1e-5)
# output calculation
out = attn @ v_reshaped # (B, H, T, d_k)
out = out.transpose(1,2).contiguous().view(B, T, d) # (B, T, d) ---> put together all the heads
out = self.out(out)
return out
3. Training¶
3.1. Preparing the dataset¶
class DeEnPairs(Dataset):
def __init__(self, dataset):
self.de = dataset["de"]
self.en = dataset["en"]
def __len__(self):
return len(self.de)
def __getitem__(self, i):
return self.de[i], self.en[i]
def make_causal_collate(tok, block_size=256, train_on_source=False):
PAD_id = tok.pad_token_id
BOS_id = tok.bos_token_id
EOS_id = tok.eos_token_id
def encode_plain(text):
# Raw subword IDs, no BOS/EOS added automatically
return tok(text, add_special_tokens=False)["input_ids"]
def collate(batch):
input_ids_list, labels_list, attn_list, end_of_DE_list = [], [], [], []
for de_txt, en_txt in batch:
de_ids = encode_plain(de_txt)
en_ids = encode_plain(en_txt)
# Build: [de, BOS, en, EOS]
seq = de_ids + [BOS_id] + en_ids + [EOS_id]
x = torch.tensor(seq, dtype=torch.long)
# mask source part (German + the BOS boundary) unless you also want LM on DE
# find BOS position we inserted as English boundary
bos_pos = (x == BOS_id).nonzero(as_tuple=True)[0][0].item()
# Labels = next-token targets. we shift inputs by one implicitly via CE on logits[:, :-1] vs labels[:, 1:]
y = x.clone()[1:]
if not train_on_source:
y[:bos_pos] = -100 # ignore German and the BOS token
# last token has no next-token label; safe to keep (HF shifts internally),
# but many people prefer to mask last position explicitly:
# y[-1] = -100
attn = torch.ones_like(x, dtype=torch.long) # 1 for real tokens; padding will be 0
input_ids_list.append(x)
labels_list.append(y)
attn_list.append(attn)
end_of_DE_list.append(bos_pos+1)
# Pad to batch max length
input_ids = pad_sequence(input_ids_list, batch_first=True, padding_value=PAD_id)
labels = pad_sequence(labels_list, batch_first=True, padding_value=-100)
attention = pad_sequence(attn_list, batch_first=True, padding_value=0)
end_of_DE_list = torch.tensor(end_of_DE_list, dtype=torch.long)
# If sequence still exceeds block_size after padding logic (rare), hard cut at right edge:
if input_ids.size(1) > block_size:
input_ids = input_ids[:, -block_size:]
labels = labels[:, -block_size:]
attention = attention[:, -block_size:]
return {"input_ids": input_ids, "attention_mask": attention, "labels": labels, "end_of_DE": end_of_DE_list}
return collate
train_ds = DeEnPairs(ds_train)
valid_ds = DeEnPairs(ds_valid)
collate = make_causal_collate(tok, block_size=256, train_on_source=True)
train_dl = DataLoader(train_ds, batch_size=64, shuffle=True, collate_fn=collate)
batch = next(iter(train_dl))
# 1 if there is a real token, 0 if padding
print('Attention masks:\n',batch['attention_mask'][0],'\n')
# indices of tokens in the vocabulary. remember 58101 is <bos>, 0 is <eos>, 58100 is <pad>
print('Input ids:\n',batch['input_ids'][0],'\n')
# the beginning idx of the English part (after German + <bos>)
print('End of German sentences:\n',batch['end_of_DE'][0],'\n')
# the idx of the next token to predict, -100 if ignored (German + <bos> + padding)
print('Labels:\n',batch['labels'][0],'\n')
# print the actual text
for i in range(batch['attention_mask'][0].sum()):
print(batch['input_ids'][0][i].item(), tok.decode(batch['input_ids'][0][i].item()), sep='\t')
Attention masks:
tensor([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0])
Input ids:
tensor([ 525, 17593, 222, 41377, 15, 19943, 16778, 37, 94, 16167,
2, 145, 2229, 12317, 4691, 22799, 3, 58101, 93, 17,
7565, 18, 7, 39, 17, 6409, 15, 1730, 175, 17,
6, 9401, 32, 14, 17, 12662, 5, 17, 9691, 7,
88, 1032, 17, 19376, 17, 27499, 17, 16391, 6, 3,
0, 58100, 58100, 58100, 58100, 58100, 58100, 58100, 58100, 58100,
58100, 58100, 58100, 58100, 58100, 58100, 58100, 58100, 58100, 58100,
58100, 58100, 58100, 58100, 58100])
End of German sentences:
tensor(18)
Labels:
tensor([17593, 222, 41377, 15, 19943, 16778, 37, 94, 16167, 2,
145, 2229, 12317, 4691, 22799, 3, 58101, 93, 17, 7565,
18, 7, 39, 17, 6409, 15, 1730, 175, 17, 6,
9401, 32, 14, 17, 12662, 5, 17, 9691, 7, 88,
1032, 17, 19376, 17, 27499, 17, 16391, 6, 3, 0,
-100, -100, -100, -100, -100, -100, -100, -100, -100, -100,
-100, -100, -100, -100, -100, -100, -100, -100, -100, -100,
-100, -100, -100, -100])
525 Eine
17593 Figur
222 eines
41377 orientalisch
15 en
19943 Mannes
16778 sitzt
37 auf
94 einer
16167 Mauer
2 ,
145 vor
2229 einigen
12317 weißen
4691 Wohn
22799 häusern
3 .
58101 <bos>
93 A
17
7565 figur
18 e
7 of
39 an
17
6409 ori
15 en
1730 tal
175 man
17
6 s
9401 its
32 on
14 a
17
12662 wall
5 in
17
9691 front
7 of
88 so
1032 me
17
19376 white
17
27499 apartment
17
16391 building
6 s
3 .
0 </s>
3.2. Our training pipeline¶
In practice, we train these models efficiently by predicting many next tokens in parallel. Suppose our target sequence has length D. Instead of creating D separate training examples (each with a different context), we process the whole sequence at once. We feed the model the input [x₁, x₂, …, x_{D-1}], and we ask it to predict [x₂, x₃, …, x_D]. In other words, for every position, the model tries to guess “what comes next.” This produces D-1 predictions from a single forward pass. During inference, the model still generates one token at a time, but during training we can supervise all positions simultaneously, which makes learning much faster. The important distinction is: training = parallel next-token prediction across the sequence, generation = sequential prediction, one token at a time.
So now, we implement a causal attention mechanism that predicts token $i$ conditioned to all tokens until $i$.
class MultiHeadCausalSelfAttention(nn.Module):
def __init__(self, d, H):
''' Multi-Head Self-Attention module.
Args:
d: Embedding dimension.
H: Number of attention heads.
'''
super(MultiHeadCausalSelfAttention, self).__init__()
assert d % H == 0, "Embedding dimension must be divisible by number of heads."
self.d = d
self.H = H
self.d_k = d // H # Dimension per head
self.qkv = nn.Linear(d, 3*d) # Combined query, key, value projection
self.out = nn.Linear(d, d) # Output projection
def forward(self, X):
'''
Forward pass through the Multi-Head Self-Attention module.
Args:
X: Input tensor of shape (B, T, d).
eng_start_idx: Tensor of shape (B,) indicating the start index of the English part in each sequence.
Returns:
Output tensor of shape (B, T, d).
'''
B, T, d = X.shape
assert d == self.d, f'Input embedding dimension {d} does not match model dimension {self.d}.'
# Linear projections
qkv = self.qkv(X)
q,k,v = qkv.chunk(3, dim=-1) # Each is (B, T, d) ---> form queries, keys, values
# split into heads
q_reshaped = q.view(B, T, self.H, self.d_k).transpose(1,2) # (B, H, T, d_k)
k_reshaped = k.view(B, T, self.H, self.d_k).transpose(1,2) # (B, H, T, d_k)
v_reshaped = v.view(B, T, self.H, self.d_k).transpose(1,2) # (B, H, T, d_k)
# Scaled dot-product attention
k_transpose = k_reshaped.transpose(-2, -1) # (B, H, d_k, T)
QK = q_reshaped @ k_transpose # (B, H, T, T) ---> QK[b,h,i] stores the similarity of token i to all tokens in the sequence
# create the causal mask
causal_mask = torch.tril(torch.ones((T, T), device=X.device)).unsqueeze(0).unsqueeze(0) # (1, 1, T, T)
QK = QK.masked_fill(causal_mask == 0, float('-inf'))
attn = QK.softmax(dim=-1) # (B, H, T, T) ---> attn[b,h,i] stores how much token i attends to all tokens in the sequence
# output calculation
out = attn @ v_reshaped # (B, H, T, d_k)
out = out.transpose(1,2).contiguous().view(B, T, d) # (B, T, d) ---> put together all the heads
out = self.out(out)
return out
3.3. Build the network¶
T = 256 # Context length (sequence length)
V = len(tok) # Vocabulary size (for embeddings)
N = 12 # Number of Transformer blocks
d = 256 # Embedding dimension
H = 8 # Number of attention heads
input_emb = create_embedding(V, d) # Input embedding
pos_emb = create_embedding(T, d) # Positional embedding
mhsa = MultiHeadCausalSelfAttention(d, H)
transf_block = Block(mhsa, d, 4*d, dropout=0.1)
norm_layer = nn.LayerNorm(d)
output_layer = nn.Linear(d, V) # Output layer to project to vocabulary size
model = TransformerNetwork(
T=T, # max seq length
N=N, # num transformer blocks
input_emb=input_emb, # Input embedding layer/module.
pos_emb=pos_emb, # Positional embedding layer/module.
transf_block=transf_block, # A single Transformer block (to be repeated N times).
norm_layer=norm_layer, # Normalization layer/module (e.g., LayerNorm).
output_layer=output_layer # Output layer/module (e.g., to map to data space).
)
print(model)
print('Number of parameters in the model:', sum(p.numel() for p in model.parameters()) )
optimizer = torch.optim.AdamW(model.parameters(), lr=5e-4, weight_decay=1e-3, betas=(0.9, 0.99), eps=1e-8)
model = model.to(device)
# state = torch.load('transformer_deen_T256_N12_d256_H8_can_generate_german.pth', map_location=device)
# model.load_state_dict(state)
TransformerNetwork(
(input_emb): Embedding(58102, 256)
(pos_emb): Embedding(256, 256)
(transf_blocks): ModuleList(
(0-11): 12 x Block(
(mhsa): MultiHeadCausalSelfAttention(
(qkv): Linear(in_features=256, out_features=768, bias=True)
(out): Linear(in_features=256, out_features=256, bias=True)
)
(ffn): Sequential(
(0): Linear(in_features=256, out_features=1024, bias=True)
(1): ReLU()
(2): Linear(in_features=1024, out_features=256, bias=True)
)
(norm1): LayerNorm((256,), eps=1e-05, elementwise_affine=True)
(norm2): LayerNorm((256,), eps=1e-05, elementwise_affine=True)
(dropout): Dropout(p=0.1, inplace=False)
)
)
(norm_layer): LayerNorm((256,), eps=1e-05, elementwise_affine=True)
(output_layer): Linear(in_features=256, out_features=58102, bias=True)
)
Number of parameters in the model: 30662134
/tmp/ipykernel_616401/352975203.py:33: FutureWarning: You are using `torch.load` with `weights_only=False` (the current default value), which uses the default pickle module implicitly. It is possible to construct malicious pickle data which will execute arbitrary code during unpickling (See https://github.com/pytorch/pytorch/blob/main/SECURITY.md#untrusted-models for more details). In a future release, the default value for `weights_only` will be flipped to `True`. This limits the functions that could be executed during unpickling. Arbitrary objects will no longer be allowed to be loaded via this mode unless they are explicitly allowlisted by the user via `torch.serialization.add_safe_globals`. We recommend you start setting `weights_only=True` for any use case where you don't have full control of the loaded file. Please open an issue on GitHub for any issues related to this experimental feature.
state = torch.load('transformer_deen_T256_N12_d256_H8_can_generate_german.pth', map_location=device)
--------------------------------------------------------------------------- NameError Traceback (most recent call last) Cell In[9], line 35 33 state = torch.load('transformer_deen_T256_N12_d256_H8_can_generate_german.pth', map_location=device) 34 model.load_state_dict(state) ---> 35 print(aaa) NameError: name 'aaa' is not defined
3.4. Train the network¶
# train the network
for epoch in range(20):
model.train()
total_loss = 0.0
for i,batch in enumerate(train_dl):
input_ids = batch['input_ids'].to(device)
labels = batch['labels'].to(device)
eng_start_idx = batch['end_of_DE'].to(device)
optimizer.zero_grad()
outputs = model(input_ids) # (B, T, V)
logits = outputs[:, :-1, :].contiguous() # (B, T-1, V)
loss = F.cross_entropy(logits.view(-1, V), labels.view(-1), ignore_index=-100)
loss.backward()
optimizer.step()
total_loss += loss.item()
if i % 100 == 0:
print(f'Processing batch {i}/{len(train_dl)}. Mean loss so far: {total_loss/(i+1):.4f}')
avg_loss = total_loss / len(train_dl)
print(f'Epoch {epoch+1}, Training Loss: {avg_loss:.4f}')
torch.save(model.state_dict(), 'transformer_deen.pth')
Processing batch 0/454. Mean loss so far: 11.1316 Processing batch 100/454. Mean loss so far: 6.0472 Processing batch 200/454. Mean loss so far: 5.1690 Processing batch 300/454. Mean loss so far: 4.7178 Processing batch 400/454. Mean loss so far: 4.4251 Epoch 1, Training Loss: 4.3016 Processing batch 0/454. Mean loss so far: 3.5583 Processing batch 100/454. Mean loss so far: 3.2004 Processing batch 200/454. Mean loss so far: 3.1463 Processing batch 300/454. Mean loss so far: 3.1020 Processing batch 400/454. Mean loss so far: 3.0596 Epoch 2, Training Loss: 3.0323 Processing batch 0/454. Mean loss so far: 2.8784 Processing batch 100/454. Mean loss so far: 2.7206 Processing batch 200/454. Mean loss so far: 2.6985 Processing batch 300/454. Mean loss so far: 2.6770 Processing batch 400/454. Mean loss so far: 2.6592 Epoch 3, Training Loss: 2.6491 Processing batch 0/454. Mean loss so far: 2.4186 Processing batch 100/454. Mean loss so far: 2.4207 Processing batch 200/454. Mean loss so far: 2.4191 Processing batch 300/454. Mean loss so far: 2.4177 Processing batch 400/454. Mean loss so far: 2.4111 Epoch 4, Training Loss: 2.4055 Processing batch 0/454. Mean loss so far: 2.1825 Processing batch 100/454. Mean loss so far: 2.2375 Processing batch 200/454. Mean loss so far: 2.2403 Processing batch 300/454. Mean loss so far: 2.2430 Processing batch 400/454. Mean loss so far: 2.2384 Epoch 5, Training Loss: 2.2337 Processing batch 0/454. Mean loss so far: 2.2638 Processing batch 100/454. Mean loss so far: 2.0781 Processing batch 200/454. Mean loss so far: 2.0903 Processing batch 300/454. Mean loss so far: 2.0961 Processing batch 400/454. Mean loss so far: 2.1039 Epoch 6, Training Loss: 2.1036 Processing batch 0/454. Mean loss so far: 2.0014 Processing batch 100/454. Mean loss so far: 1.9786 Processing batch 200/454. Mean loss so far: 1.9838 Processing batch 300/454. Mean loss so far: 1.9911 Processing batch 400/454. Mean loss so far: 1.9965 Epoch 7, Training Loss: 1.9970 Processing batch 0/454. Mean loss so far: 1.9444 Processing batch 100/454. Mean loss so far: 1.8606 Processing batch 200/454. Mean loss so far: 1.8752 Processing batch 300/454. Mean loss so far: 1.8913 Processing batch 400/454. Mean loss so far: 1.8993 Epoch 8, Training Loss: 1.9066 Processing batch 0/454. Mean loss so far: 1.6859 Processing batch 100/454. Mean loss so far: 1.7814 Processing batch 200/454. Mean loss so far: 1.7992 Processing batch 300/454. Mean loss so far: 1.8133 Processing batch 400/454. Mean loss so far: 1.8245 Epoch 9, Training Loss: 1.8286 Processing batch 0/454. Mean loss so far: 1.7428 Processing batch 100/454. Mean loss so far: 1.7061 Processing batch 200/454. Mean loss so far: 1.7296 Processing batch 300/454. Mean loss so far: 1.7408 Processing batch 400/454. Mean loss so far: 1.7550 Epoch 10, Training Loss: 1.7606 Processing batch 0/454. Mean loss so far: 1.6196 Processing batch 100/454. Mean loss so far: 1.6392 Processing batch 200/454. Mean loss so far: 1.6609 Processing batch 300/454. Mean loss so far: 1.6790 Processing batch 400/454. Mean loss so far: 1.6942 Epoch 11, Training Loss: 1.7006 Processing batch 0/454. Mean loss so far: 1.5412 Processing batch 100/454. Mean loss so far: 1.5813 Processing batch 200/454. Mean loss so far: 1.6037 Processing batch 300/454. Mean loss so far: 1.6211 Processing batch 400/454. Mean loss so far: 1.6373 Epoch 12, Training Loss: 1.6448 Processing batch 0/454. Mean loss so far: 1.5117 Processing batch 100/454. Mean loss so far: 1.5385 Processing batch 200/454. Mean loss so far: 1.5619 Processing batch 300/454. Mean loss so far: 1.5775 Processing batch 400/454. Mean loss so far: 1.5889 Epoch 13, Training Loss: 1.5935 Processing batch 0/454. Mean loss so far: 1.3743 Processing batch 100/454. Mean loss so far: 1.4866 Processing batch 200/454. Mean loss so far: 1.5096 Processing batch 300/454. Mean loss so far: 1.5286 Processing batch 400/454. Mean loss so far: 1.5441 Epoch 14, Training Loss: 1.5500 Processing batch 0/454. Mean loss so far: 1.4222 Processing batch 100/454. Mean loss so far: 1.4365 Processing batch 200/454. Mean loss so far: 1.4626 Processing batch 300/454. Mean loss so far: 1.4873 Processing batch 400/454. Mean loss so far: 1.5038 Epoch 15, Training Loss: 1.5086 Processing batch 0/454. Mean loss so far: 1.3181 Processing batch 100/454. Mean loss so far: 1.4103 Processing batch 200/454. Mean loss so far: 1.4276 Processing batch 300/454. Mean loss so far: 1.4486 Processing batch 400/454. Mean loss so far: 1.4640 Epoch 16, Training Loss: 1.4719 Processing batch 0/454. Mean loss so far: 1.3642 Processing batch 100/454. Mean loss so far: 1.3767 Processing batch 200/454. Mean loss so far: 1.3968 Processing batch 300/454. Mean loss so far: 1.4167 Processing batch 400/454. Mean loss so far: 1.4323 Epoch 17, Training Loss: 1.4374 Processing batch 0/454. Mean loss so far: 1.3088 Processing batch 100/454. Mean loss so far: 1.3422 Processing batch 200/454. Mean loss so far: 1.3636 Processing batch 300/454. Mean loss so far: 1.3824 Processing batch 400/454. Mean loss so far: 1.3981 Epoch 18, Training Loss: 1.4056 Processing batch 0/454. Mean loss so far: 1.2703 Processing batch 100/454. Mean loss so far: 1.3162 Processing batch 200/454. Mean loss so far: 1.3311 Processing batch 300/454. Mean loss so far: 1.3505 Processing batch 400/454. Mean loss so far: 1.3692 Epoch 19, Training Loss: 1.3765 Processing batch 0/454. Mean loss so far: 1.2532 Processing batch 100/454. Mean loss so far: 1.2835 Processing batch 200/454. Mean loss so far: 1.3037 Processing batch 300/454. Mean loss so far: 1.3248 Processing batch 400/454. Mean loss so far: 1.3416 Epoch 20, Training Loss: 1.3480
3.5. Example model outputs¶
Finally, we take a test input and let model translate it. We give the German sentences as input and let model predict the next tokens.
@torch.no_grad()
def generate(model, idx, max_new_tokens, temperature=1.0, do_sample=False, top_k=None):
"""
Parameters:
-----------
model: The trained Transformer model.
idx: Tensor of shape (B, T) containing the initial sequence of token indices.
max_new_tokens: Number of new tokens to generate.
temperature: Controls the randomness of predictions by scaling the logits.
do_sample: If True, sample from the probability distribution; if False, take the most likely token.
top_k: If specified, restricts sampling to the top_k most probable tokens
"""
for _ in range(max_new_tokens):
# forward the model to get the logits for the index in the sequence
logits = model(idx)
# pluck the logits at the final step and scale by desired temperature
logits = logits[:, -1, :] / temperature
# optionally crop the logits to only the top k options
if top_k is not None:
v, _ = torch.topk(logits, top_k)
logits[logits < v[:, [-1]]] = -float('Inf')
# apply softmax to convert logits to (normalized) probabilities
probs = F.softmax(logits, dim=-1)
# either sample from the distribution or take the most likely element
if do_sample:
idx_next = torch.multinomial(probs, num_samples=1)
else:
_, idx_next = torch.topk(probs, k=1, dim=-1)
# append sampled index to the running sequence and continue
idx = torch.cat((idx, idx_next), dim=1)
return idx
# generate starting from a test sentence
valid_dl = DataLoader(valid_ds, batch_size=64, shuffle=True, collate_fn=collate)
batch = next(iter(valid_dl))
i = 0
input_ids, attention_mask, end_of_de = batch['input_ids'][i:i+1], batch['attention_mask'][i:i+1], batch['end_of_DE'][i:i+1]
input_ids, attention_mask, end_of_de = input_ids.to(device), attention_mask.to(device), end_of_de.to(device)
# translate
print('Input:\t\t', tok.decode(input_ids[0,:end_of_de]))
print('Output:\t\t', tok.decode(input_ids[0][end_of_de:]))
model_output = generate(model, input_ids[:,:end_of_de], 50, temperature=1.0, do_sample=False, top_k=None)
print('Generated:\t', tok.decode(model_output[0][end_of_de:]))
# generate German sentence
# print('Input:\t\t', tok.decode(input_ids[0,:end_of_de//2]))
# print('Output:\t\t', tok.decode(input_ids[0][end_of_de//2:]))
# model_output = generate(model, input_ids[:,:end_of_de//2], 50, temperature=1.0, do_sample=False, top_k=None)
# print('Generated:\t', tok.decode(model_output[0][end_of_de//2:]))
Input: Zwei Männer sind an einem hellen, sonnigen Tag unterwegs, um ein paar Fische im See zu fangen.<bos> Output: Two men are out on a bright, sunny day attempting to catch some fish on the lake.</s> <pad> <pad> <pad> <pad> <pad> <pad> <pad> <pad> <pad> <pad> <pad> <pad> <pad> <pad> Generated: Two men are enjoying a bright pond down a sideway toy in lake a lake.</s> e store's lake.</s> e store.</s> es.</s> es
4. Vision transformers¶
Vision Transformers (ViTs) bring the transformer architecture—originally designed for natural language processing—into computer vision. Instead of processing images with convolutional filters, a ViT splits an image into fixed-size patches (for example, 16×16 pixels), flattens them, and linearly projects each patch into an embedding vector. These embeddings form a sequence, much like a sentence in NLP, and are fed into a transformer encoder. A special “class token” is prepended to the sequence and its final hidden state serves as the representation for the whole image, which can then be used for classification or downstream tasks. Positional encodings are also added, since transformers themselves have no inherent sense of order or spatial arrangement.
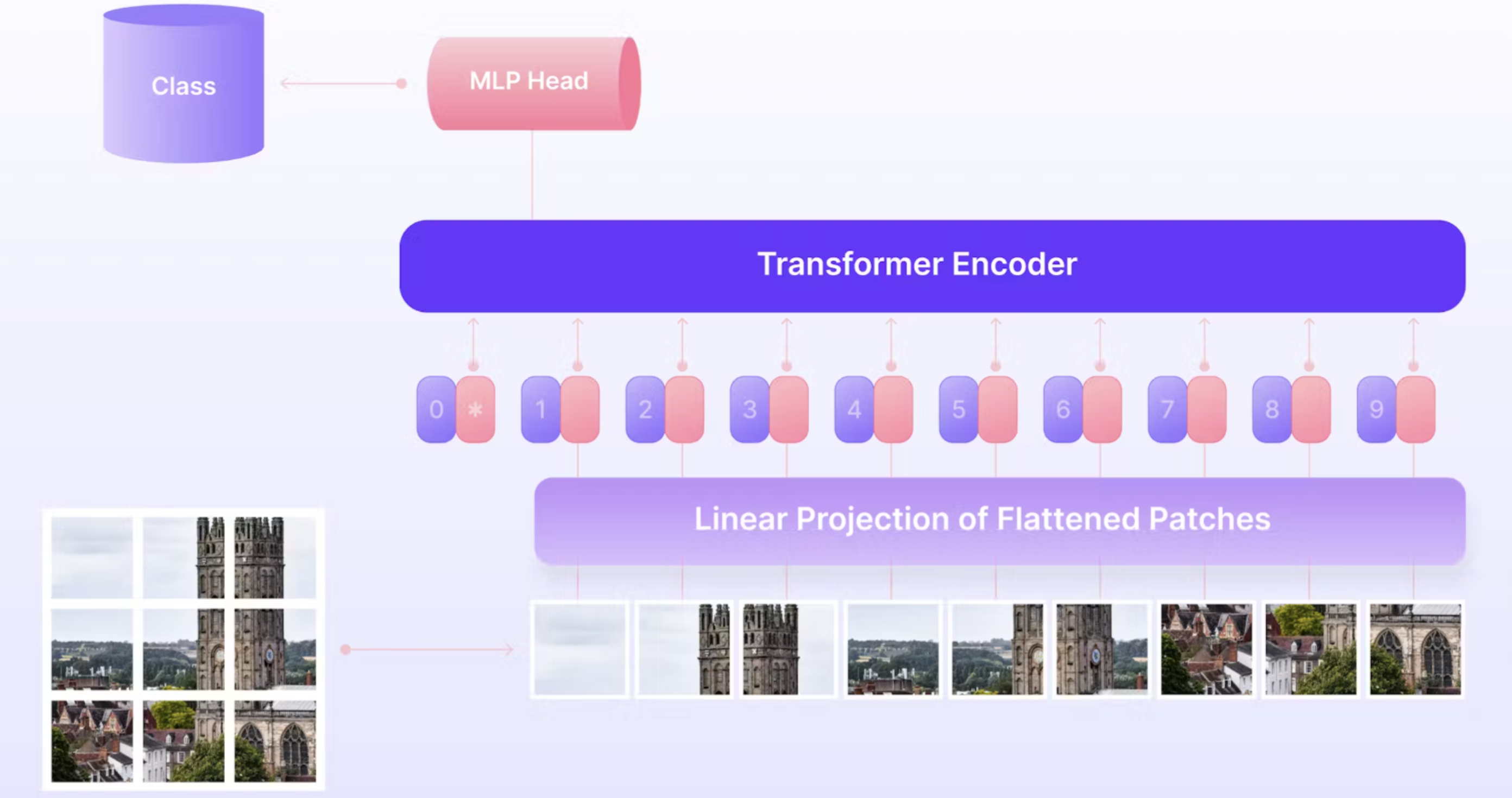
A demonstration of vision transformers (image from https://encord.com/blog/vision-transformers/)
What makes ViTs powerful is their ability to model long-range dependencies: any patch can attend to any other patch, allowing the network to capture global structure in an image. Unlike convolutional networks, which focus on local receptive fields and build hierarchical features layer by layer, ViTs start with a global receptive field from the very first layer. This flexibility comes at the cost of needing large amounts of data (or pretraining on large datasets like ImageNet-21k) and careful regularization. Once pretrained, ViTs transfer very well across tasks, and they’ve become state-of-the-art not just in classification, but also in detection, segmentation, and even generative vision models.
4.1. ViT implementation¶
The main difference to previous implementation is the addition of the CLS token.
class VisionTransformer(nn.Module):
def __init__(self, T, N, input_emb, pos_emb, transf_block, norm_layer, output_layer):
''' Transformer network with N blocks, context length T, and given components.
Args:
T: Context length (sequence length).
N: Number of Transformer blocks.
input_emb: Input embedding layer/module.
pos_emb: Positional embedding layer/module.
transf_block: A single Transformer block (to be repeated N times).
norm_layer: Normalization layer/module (e.g., LayerNorm).
output_layer: Output layer/module (e.g., for classification or regression).
'''
super(VisionTransformer, self).__init__()
self.T = T
self.input_emb = input_emb
self.pos_emb = pos_emb
self.transf_blocks = nn.ModuleList([transf_block for _ in range(N)])
self.norm_layer = norm_layer
self.output_layer = output_layer
embed_dim = pos_emb.embedding_dim
self.cls_token = nn.Parameter(torch.randn(1,1,embed_dim))
@property
def device(self):
return next(self.parameters()).device
@property
def dtype(self):
return next(self.parameters()).dtype
@property
def num_layers(self):
return len(self.transf_blocks)
@property
def d(self):
return self.input_emb.embedding_dim
def forward(self, X):
'''
Forward pass through the Transformer network.
Args:
X: Input tensor of shape (batch_size, seq_length, input_dim), or (B,T,d).
Returns:
Output tensor after passing through the Transformer network - [B,output_dim].
'''
device = X.device
B,T = X.shape[0:2]
# Input embedding
X = self.input_emb(X) # B,T,d
# add CLS token
cls_tokens = self.cls_token.repeat(B,1,1)
X = torch.cat((cls_tokens, X), dim=1)
T = T+1
# positional embeddings
P = self.pos_emb(torch.arange(T, device=device)) # T,d
P = P.unsqueeze(0).expand(B, T, -1) # B,T,d
# adding positional embeddings
X = X + P # B,T,d
# passing through Transformer blocks
for block in self.transf_blocks:
X = block(X) # B,T,d
class_token_final = X[:,0,:]
# final normalization
class_token_final = self.norm_layer(class_token_final) # B,d
# output layer
out = self.output_layer(class_token_final) # B,output_dim (depends on output_layer)
return out
4.2. Build the network¶
This time,
- the embedding layers are simple MLPs.
- input length depends on the image and patch size.
patch_size = 8
T = int((32/patch_size)**2) # Context length (sequence length)
N = 12 # Number of Transformer blocks
d = 256 # Embedding dimension
H = 16 # Number of attention heads
num_classes = 10 # number of output classes (for CIFAR-10)
input_emb = nn.Linear(3*(patch_size**2), d) # Input embedding
pos_emb = nn.Embedding(T+1, d) # create_embedding(T+1, d) # Positional embedding
mhsa = MultiHeadSelfAttention(d, H)
transf_block = Block(mhsa, d, 4*d, dropout=0.1)
norm_layer = nn.LayerNorm(d)
output_layer = nn.Linear(d, num_classes) # Output layer to project to vocabulary size
model = VisionTransformer(
T=T, # max seq length
N=N, # num transformer blocks
input_emb=input_emb, # Input embedding layer/module.
pos_emb=pos_emb, # Positional embedding layer/module.
transf_block=transf_block, # A single Transformer block (to be repeated N times).
norm_layer=norm_layer, # Normalization layer/module (e.g., LayerNorm).
output_layer=output_layer # Output layer/module (e.g., to map to data space).
)
print(model)
print('Number of parameters in the model:', sum(p.numel() for p in model.parameters()) )
optimizer = torch.optim.AdamW(model.parameters(), lr=1e-3, weight_decay=1e-3, betas=(0.9, 0.99), eps=1e-8)
model = model.to(device)
VisionTransformer(
(input_emb): Linear(in_features=192, out_features=256, bias=True)
(pos_emb): Embedding(17, 256)
(transf_blocks): ModuleList(
(0-11): 12 x Block(
(mhsa): MultiHeadSelfAttention(
(qkv): Linear(in_features=256, out_features=768, bias=True)
(out): Linear(in_features=256, out_features=256, bias=True)
)
(ffn): Sequential(
(0): Linear(in_features=256, out_features=1024, bias=True)
(1): ReLU()
(2): Linear(in_features=1024, out_features=256, bias=True)
)
(norm1): LayerNorm((256,), eps=1e-05, elementwise_affine=True)
(norm2): LayerNorm((256,), eps=1e-05, elementwise_affine=True)
(dropout): Dropout(p=0.1, inplace=False)
)
)
(norm_layer): LayerNorm((256,), eps=1e-05, elementwise_affine=True)
(output_layer): Linear(in_features=256, out_features=10, bias=True)
)
Number of parameters in the model: 846858
4.3. Training functions¶
We train the model on CIFAR10 dataset.
test_transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize([0.49139968, 0.48215841, 0.44653091], [0.24703223, 0.24348513, 0.26158784])
])
# For training, we add some augmentation. Networks are too powerful and would overfit.
train_transform = transforms.Compose([transforms.RandomHorizontalFlip(),
transforms.RandomResizedCrop((32,32),scale=(0.8,1.0),ratio=(0.9,1.1)),
transforms.ToTensor(),
transforms.Normalize([0.49139968, 0.48215841, 0.44653091], [0.24703223, 0.24348513, 0.26158784])
])
# Loading the training dataset. We need to split it into a training and validation part
# We need to do a little trick because the validation set should not use the augmentation.
train_dataset = CIFAR10(root='data/', train=True, transform=train_transform, download=True)
val_dataset = CIFAR10(root='data/', train=True, transform=test_transform, download=True)
train_dl = DataLoader(train_dataset, batch_size=128, shuffle=True, num_workers=2, pin_memory=True)
val_dl = DataLoader(val_dataset, batch_size=256, shuffle=False, num_workers=2, pin_memory=True)
def img_to_patch(x, patch_size):
"""
Inputs:
x - torch.Tensor representing the image of shape [B, C, H, W]
patch_size - Number of pixels per dimension of the patches (integer)
"""
B, C, H, W = x.shape
x = x.reshape(B, C, H//patch_size, patch_size, W//patch_size, patch_size)
x = x.permute(0, 2, 4, 1, 3, 5) # [B, H', W', C, p_H, p_W]
x = x.flatten(1,2) # [B, H'*W', C, p_H, p_W]
x = x.flatten(2,4) # [B, H'*W', C*p_H*p_W]
return x
# X = img_to_patch(X, self.patch_size) # B,T,d
Files already downloaded and verified Files already downloaded and verified
4.4. Training loop¶
# train the network
for epoch in range(20):
model.train()
total_accuracy = 0.0
for i,batch in enumerate(train_dl):
X, y = batch
X, y = X.to(device), y.to(device)
X = img_to_patch(X, patch_size)
optimizer.zero_grad()
logits = model(X) # (B, num_classes)
loss = F.cross_entropy(logits, y)
accuracy = (logits.argmax(dim=-1) == y).float().mean()
loss.backward()
optimizer.step()
total_accuracy += accuracy.item()
if i % 100 == 0:
print(f'Processing batch {i}/{len(train_dl)}. Mean accuracy so far: {total_accuracy/(i+1):.4f}')
# now validate
model.eval()
total_val_accuracy = 0.0
with torch.no_grad():
for i,batch in enumerate(val_dl):
X, y = batch
X, y = X.to(device), y.to(device)
X = img_to_patch(X, patch_size)
logits = model(X) # (B, num_classes)
accuracy = (logits.argmax(dim=-1) == y).float().mean()
total_val_accuracy += accuracy.item()
print(f'Epoch {epoch+1}, Training Accuracy: {total_accuracy/len(train_dl):.4f}, Validation Accuracy: {total_val_accuracy/len(val_dl):.4f}')